Enkelvoudige, meervoudige en moderatie regressieanalyse

Inleiding

Onlangs heb ik een groep studenten van Forensische Orthopedagogiek van de Universeriteit van Amsterdam begeleid bij het schrijven van hun masterscriptie. Ze hadden met elkaar een sample verzameld. Ze moesten op zoek naar de relatie tussen cannabisgebruik en online-blootstelling aan cannabis. Daarboven op moesten ze op zoek naar of bepaalde variabelen deze invloed beïnvloeden. Daarvoor moesten ze een moderatieanalyse uitvoeren. In deze korte blog laat ik zien hoe ik deze techniek zou uitvoeren. Dat heb ik de studenten ook laten zien en hier deel ik het met anderen. Eerst introduceer ik heel kort moderatie analyse als onderdeel van regressieanalyse en wat de achterliggende ideeën ervan. Dan ligt ik kort de dataset uit die gebruikt is. Dan laat ik zien welke pakketten van R ik hierbij heb gebruikt en hoe deze pakketten ons werk hierbij kunnen ondersteunen. Dan laat ik twee soorten modernatieanalyses zien. Één analyse waarbij de moderator een categoriale variabele en een andere analyse waarbij de moderator een continue variabele is. Dan laat ik kort de tekst zien hoe de tekst er dan uitziet hier.

Moderatieanalyse

Moderatieanalyse is een vorm van regressieanalyse. Een moderator \(z\) is een variable die van invloed is op de richting en/of de sterkte van de relatie tussen een onafhankelijke variabele \(x\) en een afhankelijke variabele \(y\). Die invloed wordt gezien als interactie tussen \(x\) en \(z\) in de relatie met \(y\).

Hieronder volgen twee moderatieanalyses (eerst met een categoriale en dan een continue variabele). Elk van de moderatieanalyse wordt vergeleken met een enkelvoudige en een meervoudige regressie.

Enkelvoudige regressie (Model 1) ziet er dan zo uit:

\[y= \beta_{0} + \beta_{1} + \epsilon\] Vervolgens voegen we de variabele \(z\) eerst toe in een meervoudigige regressie (Model2) \[y= \beta_{0} + \beta_{1} + \beta_{2}{z} + \epsilon\] Dan wordt het interactieffect tussen de twee onafhankelijke variabelen toegevoegd in de moderatieanalyse (Model 3). Het interactieeffect zien we in de regressie coefficient \(\beta_{3}{x}{z}\) die het product is van de ene onafhankelijke variabele. In de analyse kijken we dan of de moderator significant is. Is dat het geval, dan kunnen we zeggen dat de moderator het verband tussen afhankelijke en onafhankelijke variabele beïnvloedt. Hier gaat het om moderatieanalyse of gemodereerde multiple regressie. Model 3 ziet er dan zo uit:

\[y= \beta_{0} + \beta_{1}{x} + \beta_{2}{z} + \beta_{3}{x}{z} + \epsilon\] Hieronder laat ik zien hoe je dat achtereenvolgens doet in R. De moderatieanalyse met een categoriale variabele is net iets anders dan een moderatieanalyse met een continue variabele. Beide laat ik hier onder zien. Eerst maar eens iets over de pakketten die ik bij de analyses heb gebruikt.

De pakketten

Voor deze analyse maak ik gebruik van enkkele pakketten die hierbij - Het pakket haven heb ik gebruikt om het spss-databestand toegankelijk voor R te maken; - Tidyverse gebruik ik voor het bewerken van het bestand maar ook om de resultaten goed te kunnen visualiseren; - De pakketten jtools en huxtable zijn gebruikt om de modellen overzichtelijk in een tabel te kunnen afddrukken; - Het pakket interactions is gebruikt om van moderatie inzichtelijke interactieplots te tonen. De pakketten moeten wel op jouw machine geïnstalleerd zijn om te kunnen gebruiken.

library(haven) # pakket om spss bestanden binnen te halen
library(tidyverse) # bekende dataverwerkingspakket

── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
✔ ggplot2 3.4.2     ✔ purrr   1.0.2
✔ tibble  3.2.1     ✔ dplyr   1.1.2
✔ tidyr   1.3.0     ✔ stringr 1.5.0
✔ readr   2.1.4     ✔ forcats 0.5.2
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()

library(jtools) # hier kunnen mooi regressie modellen mee in tabelvorm worden gebracht
library(huxtable) # werkt samen met jtools 

Attaching package: 'huxtable'

The following object is masked from 'package:dplyr':

    add_rownames

The following object is masked from 'package:ggplot2':

    theme_grey

library(interactions) # om moderatieeffecten te visualiseren 

De dataset

De dataset bestond uit 153 observaties en 79 variabelen. Laten we alleen de belangrijke variabelen binnenhalen (dataset df). Dit had ik gedaan.

df<- read_sav("Dataset Onderzoek Cannabis Scriptie.sav")

Voor mijn analyse heb ik twee uitkomstvariabelen gebruikt (gebruik van cannabis en intentie om cannabis te gebruiken), een onafhankelijke variabele (online blootstelling aan cannabisgebruik) en twee moderatoren (een categoriale en continue variabele). Ik heb de dataset kleiner gemaken en de variabelen eruit gehaald.

df<- df |>
  select(CAN, Can_intent_1, ONLINE_CAN, Ouders_can,SM_FREQ)
glimpse(df)

Ik gaf de variabelen een duidelijkere naam en gebruikte alleen kleine letters.

df<- 
  rename(df, can=CAN, can_intent=Can_intent_1, online_can=ONLINE_CAN, ouders_can=Ouders_can, sm_freq=SM_FREQ)

Van ouders die cannabis gebruikten, heb ik een dichotome variabele gemaakt (wel of niet ook gebruikt).

df<-df |>mutate(ouders_can=recode(ouders_can,
                                  `0`="niet",
                                  `1`="wel",
                                  `2`="wel",
                                  `3`="wel",
                                  `4`="wel"))

Voor de tweede analyse gebruikte ik gecentreerde variabelen. Die heb ik toegevoegd aan het databestand.

df<-df |> mutate(
  online_can_c = scale(online_can, scale = FALSE),
  sm_freq_c = scale(sm_freq, scale = FALSE)
)

Zo ziet het databestand er nu uit?

df<-read_csv('df.csv')

Rows: 153 Columns: 7
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): ouders_can
dbl (6): can, can_intent, online_can, sm_freq, online_can_c, sm_freq_c

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

glimpse(df)

Rows: 153
Columns: 7
$ can          <dbl> 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 2, 2, 0, 1, …
$ can_intent   <dbl> 1, 0, 0, 1, 0, 0, 0, 0, 4, 0, 0, 0, 2, 0, 0, 5, 4, 0, 1, …
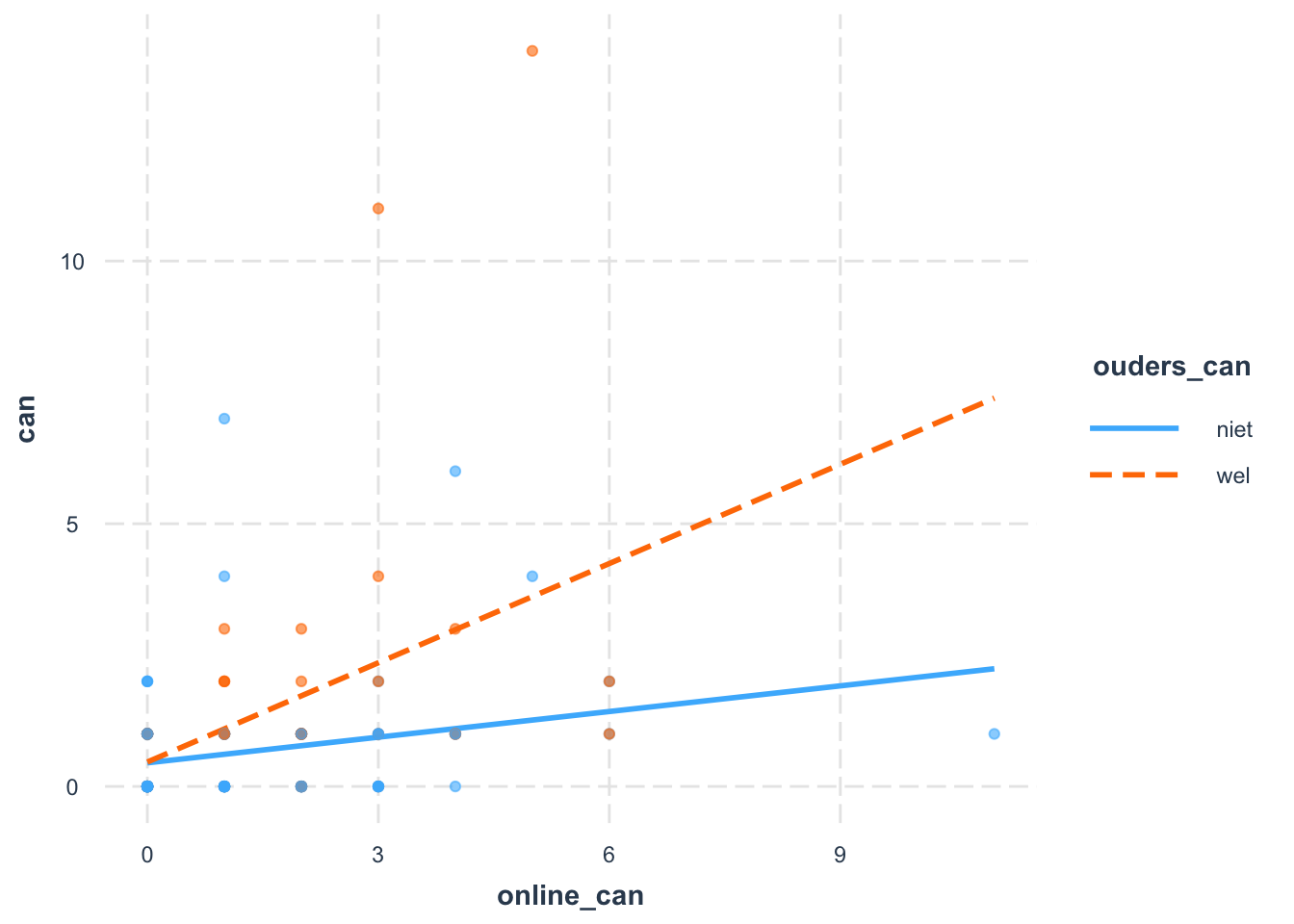
$ online_can   <dbl> NA, 3, 1, 0, 0, 2, 2, 1, 4, 2, 0, 6, 2, 4, 0, 6, 1, 0, 4,…
$ ouders_can   <chr> "niet", "wel", "niet", "niet", "niet", "niet", "wel", "ni…
$ sm_freq      <dbl> 3, 4, 4, 4, 5, 6, 4, 5, 4, 3, 4, 3, 4, 4, 3, 4, 4, 4, 4, …
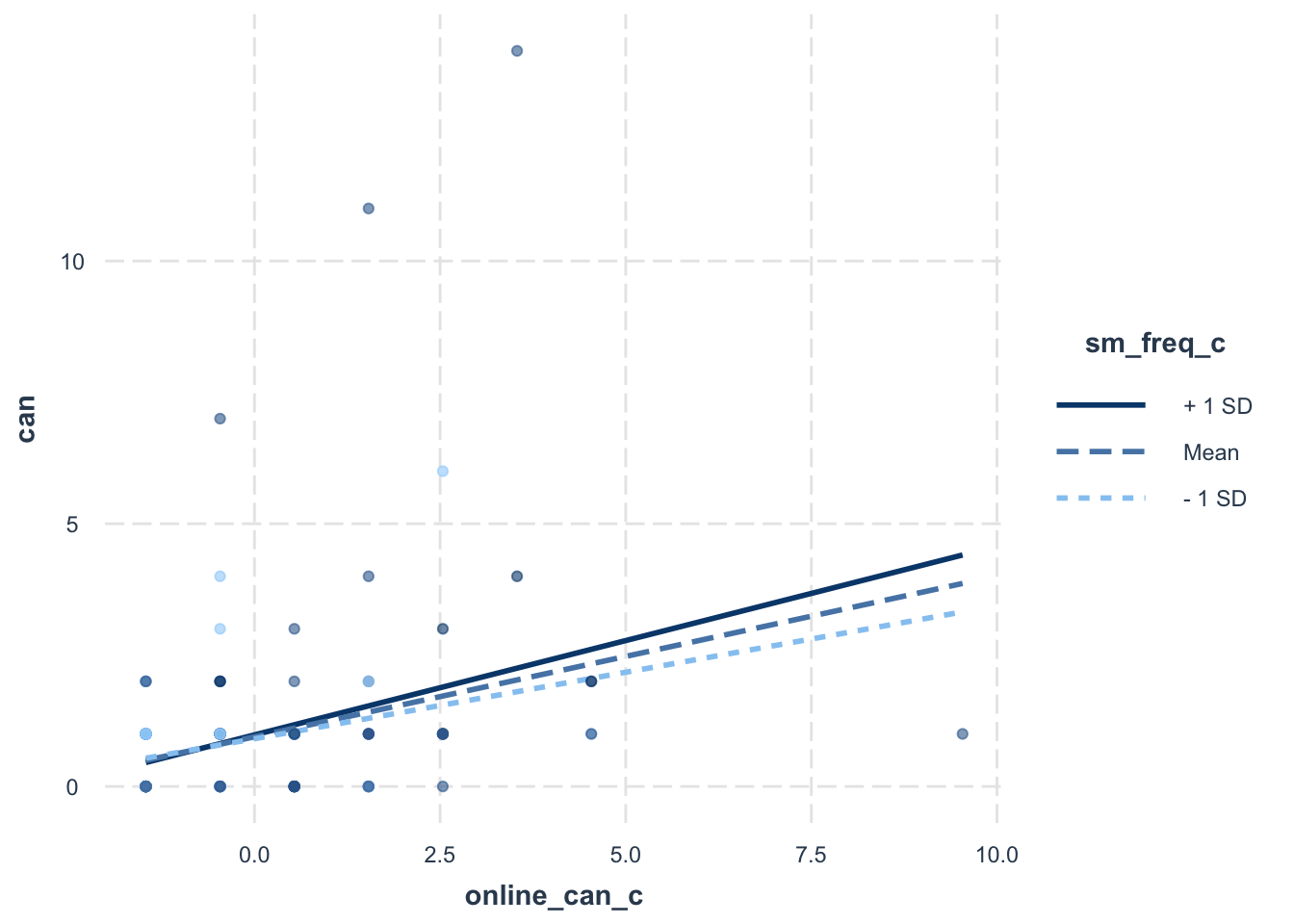
$ online_can_c <dbl> NA, 1.5367647, -0.4632353, -1.4632353, -1.4632353, 0.5367…
$ sm_freq_c    <dbl> -0.7173913, 0.2826087, 0.2826087, 0.2826087, 1.2826087, 2…

Moderatieanalyse met een continue moderator

Allereerst drie vormen van regressies rondom sociale media frequentie: enkelvoudig (met een onafhankelijke variabele), meervoudig (met twee onafhankelijke variabelem) en moderatieanalyse (interactie van de ene onafhankelijke met een andere onafhankelijke variabele).

Enkelvoudige regressie

model4 <- lm(can ~ online_can_c, data=df) 

summ(model4)

Observations	136 (17 missing obs. deleted)
Dependent variable	can
Type	OLS linear regression

F(1,134)	14.56
R²	0.10
Adj. R²	0.09

	Est.	S.E.	t val.	p
(Intercept)	0.97	0.15	6.55	0.00
online_can_c	0.33	0.09	3.82	0.00
Standard errors: OLS

Meervoudige regressie

model5 <- lm(can ~ online_can_c + sm_freq_c, data=df) 

summ(model5)

Observations	136 (17 missing obs. deleted)
Dependent variable	can
Type	OLS linear regression

F(2,133)	7.27
R²	0.10
Adj. R²	0.09

	Est.	S.E.	t val.	p
(Intercept)	0.97	0.15	6.52	0.00
online_can_c	0.32	0.09	3.56	0.00
sm_freq_c	0.07	0.24	0.30	0.76
Standard errors: OLS

Gemodereerde multiple regressie

model6 <-lm(can ~ online_can_c + sm_freq_c + online_can_c*sm_freq_c, data=df)
summ(model6)

Observations	136 (17 missing obs. deleted)
Dependent variable	can
Type	OLS linear regression

F(3,132)	4.94
R²	0.10
Adj. R²	0.08

	Est.	S.E.	t val.	p
(Intercept)	0.94	0.16	6.08	0.00
online_can_c	0.31	0.09	3.27	0.00
sm_freq_c	0.06	0.24	0.23	0.82
online_can_c:sm_freq_c	0.08	0.14	0.59	0.56
Standard errors: OLS

Als we deze modellen naast elkaar zetten, zien we dat de meervoudige en de moderatieanalyse geen significantie opleveren voor de variabelen die zijn toegevoegd.

export_summs(model4, model5, model6)

	Model 1	Model 2	Model 3
(Intercept)	0.97 ***	0.97 ***	0.94 ***
	(0.15)	(0.15)	(0.16)
online_can_c	0.33 ***	0.32 ***	0.31 **
	(0.09)	(0.09)	(0.09)
sm_freq_c		0.07	0.06
		(0.24)	(0.24)
online_can_c:sm_freq_c			0.08
			(0.14)
N	136	136	136
R2	0.10	0.10	0.10
*** p < 0.001; ** p < 0.01; * p < 0.05.

Ook de grafiek laat zien dat de regressielijnen voor de verschillende groepen vrijwel gelijk lopen (geen interactieeffect).

library(interactions)

interact_plot(model6, "online_can_c", "sm_freq_c", plot.points = TRUE)

Moderatieanalyse met een dichotome moderator

Vervolgens ga ik drie regressieanalyses uitvoeren om later de resultaten te kunnen vergelijken: enkelvoudige regressie, meervoudige regressie en moderatieanalyse met dichotome moderator.

Enkelvoudige regressie

De eerste regressie ziet er zo uit:

model1 <- lm(can ~ online_can, data=df) 

Dit zijn de resultaten. jstools geeft deze resultaten helder weer.

summ(model1)

Observations	136 (17 missing obs. deleted)
Dependent variable	can
Type	OLS linear regression

F(1,134)	14.56
R²	0.10
Adj. R²	0.09

	Est.	S.E.	t val.	p
(Intercept)	0.49	0.19	2.53	0.01
online_can	0.33	0.09	3.82	0.00
Standard errors: OLS

Meervoudige regressie

Vervolgens voeg ik er een onafhankelijke variabele aan toe:

model2 <- lm(can ~ online_can + ouders_can, data=df) 

En dat ziet er zo uit:

summ(model2)

Observations	136 (17 missing obs. deleted)
Dependent variable	can
Type	OLS linear regression

F(2,133)	10.91
R²	0.14
Adj. R²	0.13

	Est.	S.E.	t val.	p
(Intercept)	0.29	0.21	1.39	0.17
online_can	0.29	0.09	3.41	0.00
ouders_canwel	0.82	0.32	2.58	0.01
Standard errors: OLS

Gemodereerde multiple regressie

Tot slot voer ik de moderatieanalyse uit, zoals hier:

model3 <-lm(can ~ online_can + ouders_can + online_can*ouders_can, data=df)

Met dit als resultaat:

summ(model3)

Observations	136 (17 missing obs. deleted)
Dependent variable	can
Type	OLS linear regression

F(3,132)	9.63
R²	0.18
Adj. R²	0.16

	Est.	S.E.	t val.	p
(Intercept)	0.45	0.21	2.11	0.04
online_can	0.16	0.10	1.66	0.10
ouders_canwel	0.02	0.45	0.04	0.97
online_can:ouders_canwel	0.47	0.19	2.49	0.01
Standard errors: OLS

We kunnen de resultaten in een duidelijke tabel terug zien. De modellen netjes naast elkaar, met sterkte van de coëfficienten, met p-waardes en met verklaarde variantie. We zien dat model 3 duidelijk het sterkste is.

export_summs(model1, model2, model3)

	Model 1	Model 2	Model 3
(Intercept)	0.49 *	0.29	0.45 *
	(0.19)	(0.21)	(0.21)
online_can	0.33 ***	0.29 ***	0.16
	(0.09)	(0.09)	(0.10)
ouders_canwel		0.82 *	0.02
		(0.32)	(0.45)
online_can:ouders_canwel			0.47 *
			(0.19)
N	136	136	136
R2	0.10	0.14	0.18
*** p < 0.001; ** p < 0.01; * p < 0.05.

Het interactieffect is in deze grafiek goed te zien:

library(interactions)

interact_plot(model3, "online_can", "ouders_can", plot.points = TRUE)

Opzet wetenschappelijk artikel als resultaat met Quarto

De dataset kreeg ik van een van de studenten toegestuurd die in haar analyses ook deze moderatoren gebruikte (ook al had ze de eerste variabele niet dichotoom gemaakt).

Mijn analyse en haar tekst heb ik gebruikt om de resultaten ook op papier te zetten. Dat heb ik met met quarto gedaan waar je goed wetenschappelijke artikelen mee kunt maken die aan bepaalde voorwaarden moeten voldoen. De opzet en de uiteindelijke tekst met resultaten vind je hier